Representación de un enunciado en forma de tabla
A partir de la descripción verbal se puede crear una tabla poniendo parejas de valores de ambas variables. Si se parte, por ejemplo, del siguiente enunciado:
En los paquetes de galletas de cierta marca se informa del contenido calórico de ese paquete. Los paquetes que son de 3 galletas ponen 48 kcal; los de 2 galletas aportan 32 kcal; y los de 5 galletas contienen 80 kcal.
El uso de una tabla facilita el cálculo y la comprensión de la relación entre magnitudes.
| Nº de galletas |
2 |
3 |
4 |
5 |
7 |
| Energía (kcal) |
32 |
48 |
|
80 |
|
Conviene ordenar de menor a mayor según los valores de la magnitud que pondríamos en el eje horizontal. Para averiguar cuántas kilocalorías corresponden a un paquete de 4 galletas, basta con hacer el doble la energía de un paquete de 2 galletas, 32 kcal: el doble de 32 kcal es 64 kcal. Ahora, para deducir la energía que habría en uno de 7 galletas, podemos por ejemplo sumar la que aportaría un paquete de 3 galletas, 48 kcal, con la que aportaría uno de 4 galletas, 64 kcal. 48 kcal más 64 kcal son 112 kcal. Completamos ahora la tabla anterior:
| Nº de galletas |
2 |
3 |
4 |
5 |
7 |
| Energía (kcal) |
32 |
48 |
64 |
80 |
112 |
Representación gráfica de una tabla
A partir de una tabla con dos magnitudes, se puede representar en unos ejes cada par ordenado formado por un valor de una magnitud con el valor correspondiente de la otra magnitud como un punto del plano. En el ejemplo anterior:
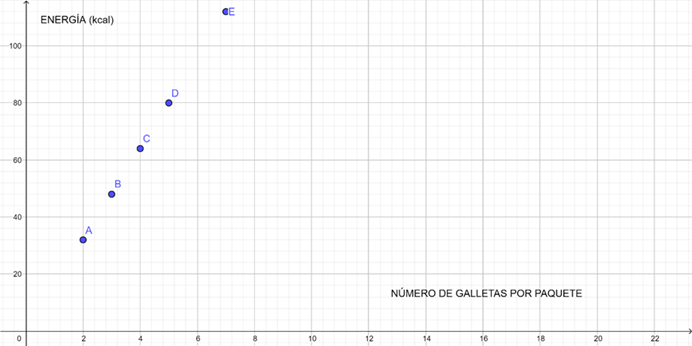
Otro ejemplo a partir del siguiente enunciado:
Un camarero tiene la costumbre de contar cuántos choques de copas hay cuando brindan entre sí todos los clientes de una mesa. Observa que cuando hay 2 clientes, hay solo 1 choque de copas; que cuando hay 3 clientes suenan 3 choques de copas; que cuando hay 4 clientes se oye 6 choques de copas; y que cuando hay 5 clientes son 10 los choques de copas. Organiza los datos de la manera que consideres más cómoda, e intenta averiguar cuántos choques habría en una mesa de 6 clientes.
Organizamos los datos en una tabla, para observar cómo evoluciona el número de choques:
| Nº de clientes |
2 |
3 |
4 |
5 |
6 |
| Nº de choques |
1 |
3 |
6 |
10 |
|
Para hallar cuántos choques habría en una mesa de 6, una manera de pensarlo es imaginar que llega con retraso un cliente a una mesa de 5: allí ya ha habido 10 choques, y ahora hay que añadir los 5 choques que tendrá que hacer educadamente el sexto cliente, con lo que serán 15 en total en la mesa de 6. La tabla quedará finalmente así:
| Nº de clientes |
2 |
3 |
4 |
5 |
6 |
| Nº de choques |
1 |
3 |
6 |
10 |
15 |
La representación gráfica de la situación anterior sería la siguiente:
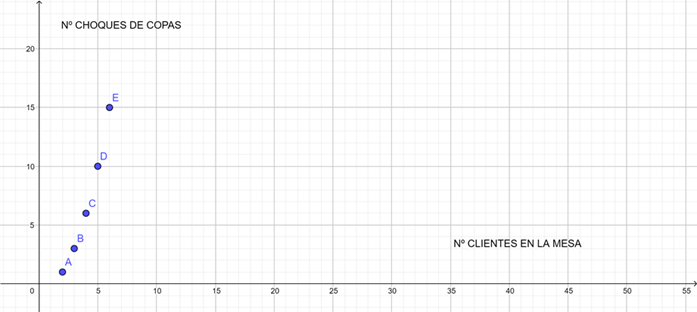
Obtención de una tabla a partir de una gráfica
En este caso basta con escribir las coordenadas de los puntos en la tabla. Por ejemplo, si tenemos representada la velocidad de un coche y el tiempo que tarda en recorrer una distancia determinada en el siguiente gráfico:
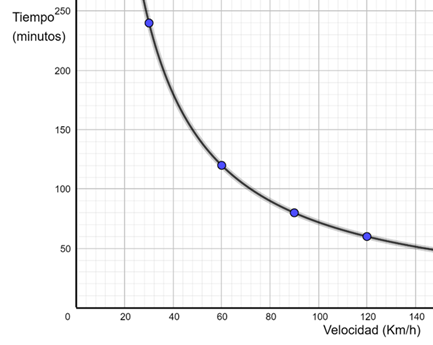
La tabla que se obtiene es:
| Velocidad (km/h) |
30 |
60 |
90 |
120 |
| Tiempo (minutos) |
240 |
120 |
80 |
60 |
Obtención de un enunciado a partir de una tabla
Analizando los valores de la tabla se puede describir la relación entre las magnitudes. Por ejemplo:
Un quiosquero quiere saber el peso de las diferentes cajas en las que le vienen las chocolatinas. Si dispone de la siguiente tabla, que relaciona el número de chocolatinas con el peso, puede deducir que el peso de cualquier número de chocolatinas se obtiene multiplicando el número de chocolatinas por el peso unitario, que es de 90 g.
| Número de chocolatinas |
1 |
5 |
10 |
20 |
| Peso (gramos) |
90 |
450 |
900 |
1800 |
Obtención de un enunciado a partir de un gráfico
Describir la relación que se observa en una gráfica con palabras, equivale a obtener el enunciado. Por ejemplo:
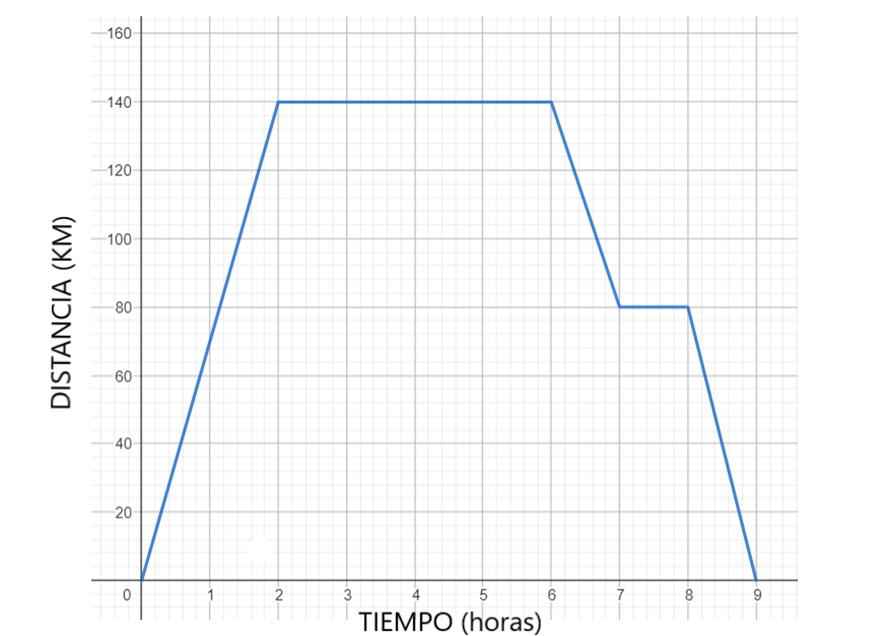
De la gráfica siguiente sobre el recorrido de Lucas hacia el campo de fútbol el día que se le olvidaron las botas en casa:
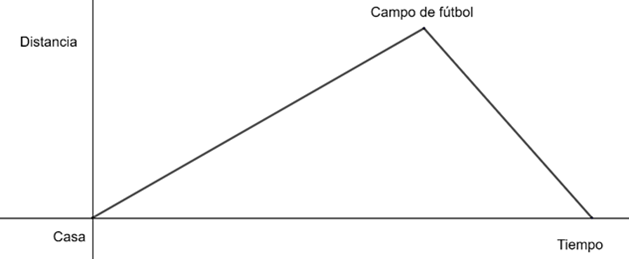
Se puede describir de la siguiente manera: “Lucas va a entrenar al campo fútbol, pero justo cuando llega al campo se da cuenta de que se le han olvidado las botas de fútbol. Corriendo vuelve a su casa a por las botas, y se sabe que va a mayor velocidad porque recorre la misma distancia en menos tiempo".