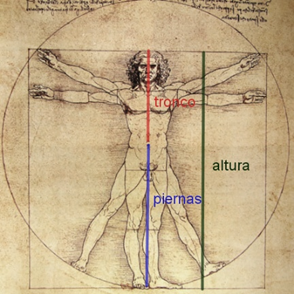
Por ejemplo, en “El hombre de Vitrubio” de Leonardo Da Vinci se cumple que la razón que forman la altura y las piernas (de los pies al ombligo) es la misma que la que forman las piernas  con el tronco (del ombligo a la cabeza), lo cual era símbolo de belleza. ¿Eres tú como el hombre de Vitrubio?

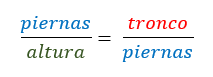
Razones y proporciones. Recuerda que en el tema de proporcionalidad has aprendido a comparar magnitudes mediante sus razones o cociente entre cantidades. En este momento puedes comparar longitudes, las de los lados de las figuras y formar con ellas una razón. También puedes ver si dos razones forman una proporción.

Semejanza. Dos figuras geométricas son iguales si tienen la misma forma y tamaño y semejantes si tienen la misma forma, pero distinto tamaño (una es el resultado de agrandar o reducir la otra sin deformarla). Por ejemplo, las figuras siguientes son todas semejantes, aunque pueda parecer que no por la posición que tienen 

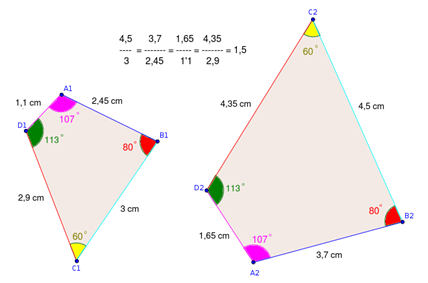Semejanza de polígonos. Para que dos polígonos sean semejantes los ángulos tienen que ser iguales y los lados correspondientes a esos ángulos tienen que ser proporcionales (forman una proporción).

Por ejemplo:

Como son dos rectángulos todos los ángulos son iguales (todos son de 90°). Veamos si los lados correspondientes están en proporción.

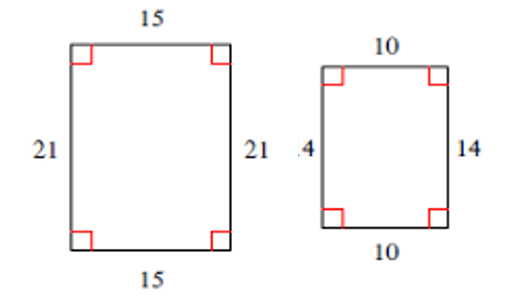
La razón entre los lados pequeños de ambos rectángulos es  10/15   o, simplificando, 2/3   .   La razón entre los lados más grandes es 24/21 ,   es decir, 2/3     . Por tanto: 10/15 = 14/21 = 2/3  .  Los lados correspondientes están en proporción.

Así, los rectángulos son semejantes y la razón de semejanza entre los lados del pequeño y del grande es 2/3 o de 2:3.

Veamos otro ejemplo:

En este caso, ¿ocurre que  18/24 = 24/36 ?     Simplificamos cada fracción:

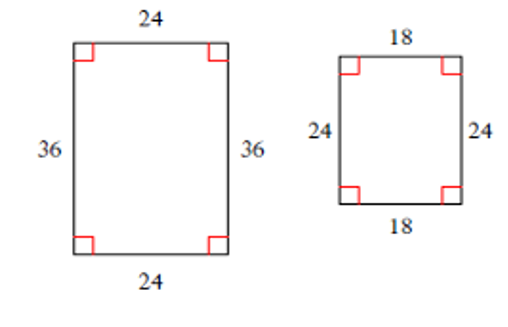
    18/24 = 3/4   y    24/36 =2/3  .

Por tanto   18/24  ≠ 24/36     . Estos rectángulos no son semejantes.

En el siguiente ejemplo tenemos dos paralelogramos. En este caso, los dos paralelogramos tienen ángulos iguales (si tienen uno tienen todos, ¿sabes por qué?) y si calculamos la razón entre lados correspondientes del grande respecto del pequeño:                                                                      

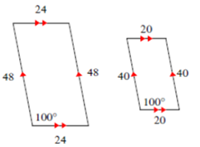             24/20 =   48/40   ya que  ambas fracciones son equivalentes a  6/5   .

                  Son polígonos semejantes y la razón de semejanza del grande respecto al pequeño es de  6:5.

. Cuando dos polígonos son semejantes se pueden calcular medidas de lados de uno de ellos si se conocen las del otro, precisamente por ser proporcionales. Por ejemplo

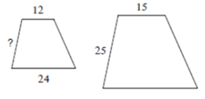
Si son semejantes, sus lados están en proporción y la razón de semejanza del pequeño respecto del grande es  12/15  , es decir, 4/5  o de 4:5. Por tanto, el lado que falta será: 

                                                                              4/5 de 25  = 4/5 .25 = 20 

En el siguiente ejemplo, la razón de semejanza de B a A  es 7:2.

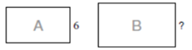Por tanto, el lado desconocido será:

7/2 de 6 =   7/2 . 6  =  21