Tales de Mileto (620-546 AC) fue un filósofo, matemático y astrónomo griego, considerado uno de los Siete Sabios de la Antigua Grecia. Busca en Internet una leyenda sobre el viaje que hizo a Egipto y entenderás el dibujo.

Existen diferentes resultados geométricos que llevan su nombre. Uno de los más conocidos es el que ahora vamos a estudiar como el teorema de Tales.

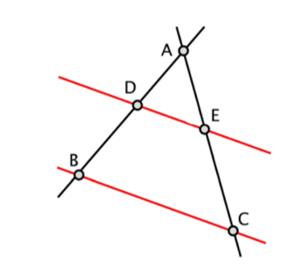“Si dos rectas no paralelas se cortan por rectas paralelas, los segmentos obtenidos en la primera son proporcionales a los correspondientes segmentos obtenidos en la segunda”.

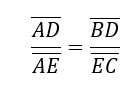
Utilizando el resultado anterior se puede demostrar que “Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado”. Dos triángulos así colocados comparten un ángulo y los lados opuestos a ese ángulo son paralelos, se dice que están en posición de Tales.

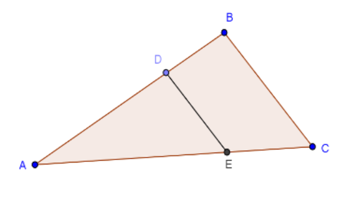
Los triángulos ADE y ABC  son semejantes, están en posición de Tales

(el ángulo A  es común y los lados DE y BC, opuestos a A, son paralelos). 

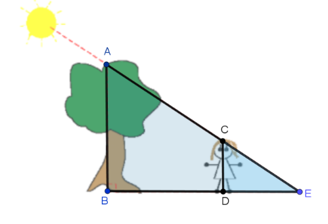
El resultado anterior se puede usar para resolver problemas como el de Sara (reto A) :

La línea CD es paralela al lado AB del triángulo grande. Por tanto, los triángulos ABE y CDE son semejantes.

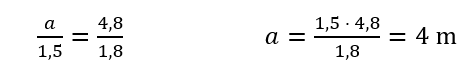
La altura del árbol es de 4 metros.

En el ejemplo de la figura los triángulos son rectángulos y comparten un ángulo. Por 

lo tanto, su tercer ángulo también es igual porque la suma de los ángulos de un triángulo es 180°. Son triángulos en posición de Tales. Triángulos semejantes.

La razón de semejanza es   9/12 o 3/4  . Esto significa que los lados del 

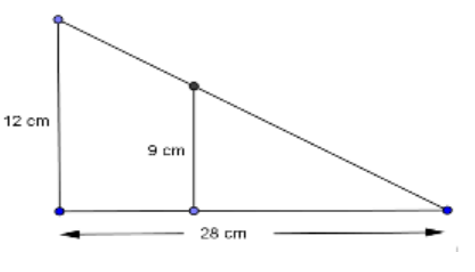
triángulo pequeño son 3/4  de los del grande.

La base del triángulo grande es 28 cm, así que la base del pequeño es 

3/4 .28 = 21 cm.

Una aplicación del teorema de Tales nos permite dividir un segmento en partes iguales. Por ejemplo,  el segmento AB se ha divido en cinco partes iguales:

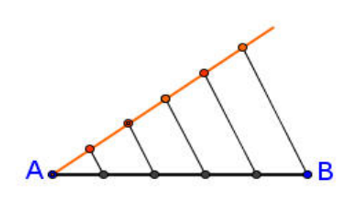
Trazamos una semirrecta a partir de A. Sobre ella marcamos, con el compás, 5 segmentos iguales, de la longitud que queramos. Unimos la última marca con B y trazamos paralelas, una por cada marca de la semirrecta