Medidas de superficie.

Empecemos por calcular la superficie que ocupa el siguiente rectángulo azul al que le hemos dividido en cuadrados iguales:

Vamos a hacernos un dibujo de nuestra mesa de clase y la dividimos en cuadrados de $1~cm$ de lado como se puede ver en la siguiente imagen:

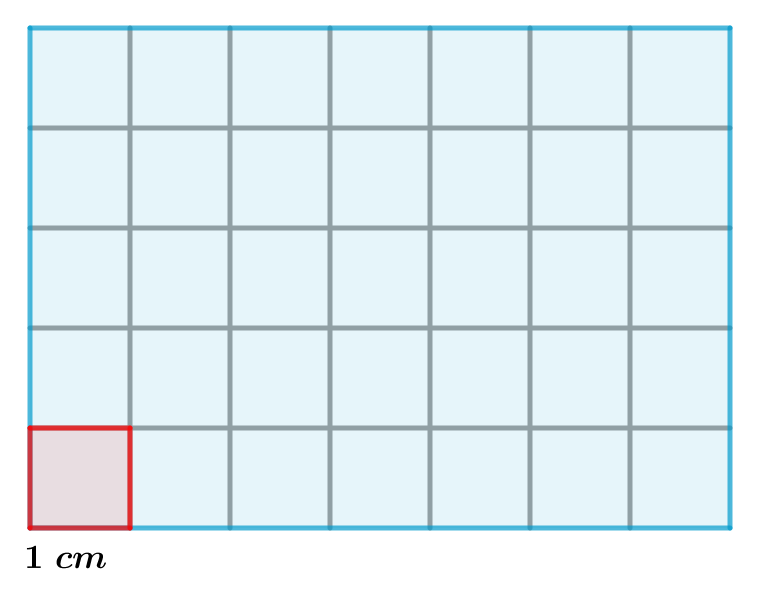
Queremos calcular su superficie. Ya no nos valen las unidades que hemos utilizado, aunque las podremos deducir de ellas.

Decíamos antes que medir es comparar lo que quiero medir con un patrón de medida. En este caso, el patrón (unidad) de medida es el cuadrado rojo, de lado $1~cm$.

El cuadrado rojo tiene $1~cm$ de lado. Diremos que su área es:

$$A=1~cm \times 1~cm=1~cm^2$$

La pregunta que nos hacemos es:

¿Cuántos cuadrados rojos de $1~cm$ de lado caben en el rectángulo azul?

La respuesta es que caben $35$ cuadrados rojos. Diremos, que la superficie del rectángulo es $35~cm^2$.

Nuestra unidad de medida es el cuadrado rojo, que tiene una superficie de $1~cm^2$ y es el que utilizaremos para comparar.

Ahora vamos a medir la superficie de nuestra mesa de clase.

Medimos el largo de la mesa: $70~cm$. Medimos el ancho: $50~cm$. En este caso dividimos la mesa en cuadrados iguales de $10~cm$ de lado:

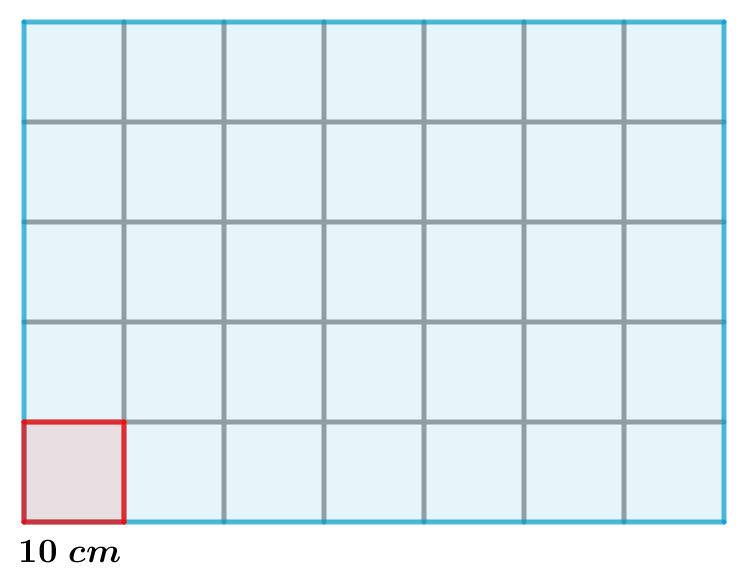
Nuestra unidad de medida es el cuadrado rojo. ¿Cuántos cuadrados caben en nuestra mesa? Caben $7 \times 5=35$ cuadrados. El área de la mesa será:

$$A=7 \times 10~cm \times 5 \times 10~cm=70~cm \times 50~cm=3 \,500~cm^2$$

Las superficies tienen dos dimensiones, para entendernos "largo" y "ancho" y la unidad base de medida de superficies va a ser el "metro cuadrado", escrito $m^2$.

A partir de la unidad base, el metro cuadrado, obtenemos sus múltiplos y submúltiplos.

Tabla de múltiplos

Prefijo	Símbolo	Factor	Verbalizo
Deca	da	$10^2=100$	Un decámetro cuadrado son $100$ metros cuadrados. Es el área de un cuadrado de $10$ metros de lado.
Hecto	h	$10^4=10\,000$	Un hectómetro cuadrado son $10\,000$ metros cuadrados. Es el área de un cuadrado de $100$ metros de lado.
Kilo	k	$10^6=1\,000\,000$	Un kilómetro cuadrado son $1\,000\,000$ metros cuadrados. Es el área de un cuadrado de $1\,000$ metros de lado.

Tabla de submúltiplos

Prefijo	Símbolo	Factor	Verbalizo
Deci	d	$10^{-2}=0,01$	Un metro cuadrado son $100$ decímetros cuadrados.
Centi	c	$10^{-4}=0,0001$	Un metro cuadrado son $10\,000$ centímetros cuadrados.
Mili	m	$10^{-6}=0,000001$	Un metro cuadrado son $1\,000\,000$ milímetros cuadrados

¿Cuál es la diferencia entre un \(dam^2\) y un \(hm^2\)

A menudo somos conscientes de la diferencia visual que hay entre un metro y un decímetro, o entre un decímetro y un centímetro, pero quizá no somos conscientes de las diferencias que se dan entre distintas unidades de superficie.

En la siguiente imagen puedes visualizar el significado de $1~dam^2$ y un $1~hm^2$, en función de los \(m^2\). Observa que el patrónn de medida, el \(m^2\) tiene distinto tamaño en las dos imágenes.

Otras unidades de superficie

Aunque no pertenece al Sistema Internacional es de uso común utilizar la hectárea para pedir grandes áreas de tierra.

Una hectárea es una medida de superficie que equivale a $10\,000~m^2$. Una hectárea equivale a un hectómetro cuadrado.