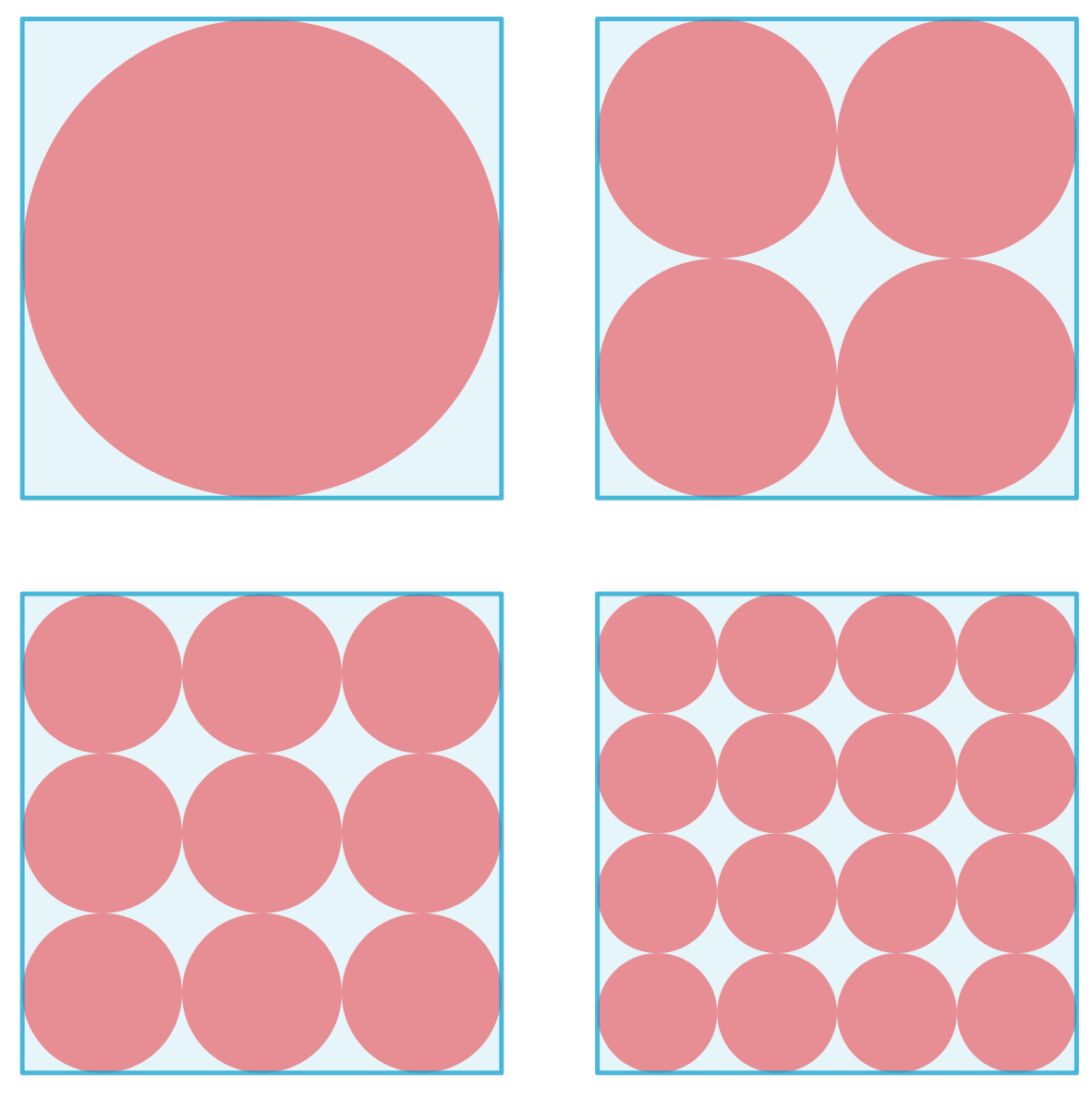
La respuesta al reto es que todos las partes sombreadas son iguales.
Llamamos \(2l \) al lado del cuadrado (generalizando), por tanto, \( l\) es la mitad lado del cuadrado.
En el primer caso el área del círculo es:
\[A_1=\pi \cdot l^2 \]
En el segundo caso, cada fila tiene 2 círculos de radio \(l/2 \). La suma de las áreas sombreadas es:
\[A_2=4 \pi \cdot \left( \frac{l}{2} \right)^2=\pi \cdot l^2 \]
En el tercer caso, cada fila tiene 3 círculos de radio \(l/3 \). La suma de las áreas sombreadas es:
\[A_3=9 \pi \cdot \left( \frac{l}{3} \right)^2=\pi \cdot l^2 \]
En el cuarto caso, cada fila tiene 4 círculos de radio \(l/4 \). La suma de las áreas sombreadas es:
\[A_4=16 \pi \cdot \left( \frac{l}{4} \right)^2=\pi \cdot l^2 \]
Es fácilmente generalizable si el cuadrado tiene \( n\) círculos de radio \(l/n \). La suma de las áreas sombreadas sería:
\[A_n=n^2 \pi \cdot \left( \frac{l}{n} \right)^2=\pi \cdot l^2 \]
NOTA: un buen ejercicio para que el alumno construya estos cuadrados y circunferencias con Geogebra.
%E9%B0%F1%F3%FC%F6%F3%F6%FD%C6%FB%FF%F7%B0%A8%A4%A2%BE%B0%F1%F3%FC%F6%F3%F6%FD%C1%FD%FE%E7%E6%FB%FD%FC%B0%A8%B0%A3%A0%A1%A6%B0%BE%B0%F1%F3%FC%F6%F3%F6%FD%DB%FC%E1%E6%E0%E7%F1%E6%FB%FD%FC%E1%B0%A8%B0%B0%BE%B0%F1%F3%FC%F6%F3%F6%FD%C0%F7%E6%E0%FD%B0%A8%B0%B0%BE%B0%F1%F3%FC%F6%F3%F6%FD%C1%FA%FD%E5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%F1%F3%FC%F6%F3%F6%FD%C0%F7%F0%FD%FD%E6%B0%A8%E6%E0%E7%F7%BE%B0%F1%F3%FC%F6%F3%F6%FD%D3%E6%E6%F7%FF%E2%E1%B0%A8%B0%A2%B0%BE%B0%F1%F3%FC%F6%F3%F6%FD%D7%E0%E0%FD%E0%DF%F7%E1%E1%F3%F5%F7%B0%A8%B0%B0%BE%B0%FF%E1%F5%E1%B0%A8%E9%B0%FF%E1%F5%DD%F9%B0%A8%B0%D3%F1%F7%E2%E6%F3%E0%B0%BE%B0%FF%E1%F5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%B0%DF%FB%FC%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%DF%F3%EA%FB%FF%FB%E8%F7%B0%A8%B0%DF%F3%EA%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%C6%FB%FF%F7%B0%A8%B0%DE%7F%FF%FB%E6%F7%B2%F6%F7%B2%E6%FB%F7%FF%E2%FD%B2%BA%FF%FF%A8%E1%E1%BB%B0%BE%B0%FF%E1%F5%DB%FC%E1%E6%E0%E7%F1%E6%FB%FD%FC%E1%B0%A8%B0%C0%F7%E6%FD%B0%BE%B0%FF%E1%F5%D4%F7%F7%F6%F0%F3%F1%F9%B0%A8%B0%C1%FD%FE%E7%F1%FBa%FC%B0%BE%B0%FF%E1%F5%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%D1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B2%F3%B2%FE%F3%B2%E1%FD%FE%E7%F1%FBa%FC%B0%BE%B0%FF%E1%F5%D7%FC%E6%F7%E0%D1%FD%F6%F7%B0%A8%B0%DB%FC%E6%E0%FD%F6%E7%E8%F1%F3%B2%F7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%D1%FD%F6%F7%B0%A8%B0%D7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B2%FC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%B0%BE%B0%FF%E1%F5%C0%F7%E3%E7%FB%E0%F7%F6%D3%F1%F1%F7%E1%E1%D9%F7%EB%B0%A8%B0%D7%E1%B2%FC%F7%F1%F7%E1%F3%E0%FB%FD%B2%F7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%C1%E7%F1%F1%F7%E1%E1%F7%E1%B0%A8%B03%D1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%D7%EA%F1%F7%FE%F7%FC%E6%F7%B3%B2%EE%B23%D5%F7%FC%FB%F3%FE%B3%B2%EE%B23%DF%E7%EB%B2%F0%FB%F7%FC%B3%B2%EE%B23%C2%F7%E0%F4%F7%F1%E6%FD%B3%B0%BE%B0%FF%E1%F5%D4%F3%FB%FE%E7%E0%F7%E1%B0%A8%B03%DC%FD%B2%F7%E0%F3%B2%F7%E1%FD%B3%B2%EE%B23%DB%FC%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DE%FD%B2%E1%F7%FC%E6%FB%FF%FD%E1%B3%B2%EE%B23%D7%E0%E0%FD%E0%B3%B0%BE%B0%FF%E1%F5%D7%C1%FA%FD%E5%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%DF%FD%E1%E6%E0%F3%E0%B2%FE%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%B0%BE%B0%FF%E1%F5%C1%E7%F0%FF%FB%E6%B0%A8%B0%D1%FD%FF%E2%E0%FD%F0%F3%E0%B0%EF%EF
Su navegador no es compatible con esta herramienta.