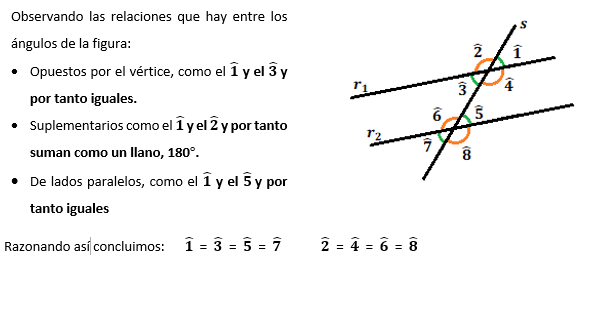
CONCEPTOS BÁSICOS Y POSICIONES DE RECTAS
CONCEPTOS BÁSICOS
A continuación vamos a trabajar utilizando la Geometría del plegado o del doblado
PLANO
Cogemos un folio y lo colocamos sobre la mesa o sobre el suelo. A continuación colocamos folios a los lados, en todas las direcciones. Así, conseguimos lo que denominamos plano: el folio colocado sobre la mesa o el suelo (no curvado) y con la posibilidad de ampliarlo en todas las direcciones
RECTA
Tomamos un folio y hacemos un doblez. Desdoblamos y marcamos el doblez con un bolígrafo. Lo que hemos marcado se denomina recta. Se designan mediante letras minúsculas. Es importante observar la condición de infinitud de la recta, consecuencia de la del plano. La recta no tiene grosor sino sólo longitud.
SEMIPLANO
Una recta divide al plano en dos partes. Cada parte, junto con la recta, se denomina semiplano.
PUNTO
Hacemos dos dobleces distintos en el folio de forma que un doblez pase sobre otro y marcamos con el bolígrafo las dos rectas respectivas r y s. Donde coinciden los dos dobleces se encuentra el punto. Punto es la intersección de dos rectas. Por tanto, el punto no tiene grosor. El punto indica una posición. Los puntos se nombran con letras mayúsculas.
SEMIRRECTA
Un punto A, sobre una recta, determina dos semirrectas. El punto A es el origen de la semirrecta, que no tiene final.
SEGMENTO
Consideramos una recta y, mediante el doblado, señalamos en ella dos puntos A y B. Se llama segmento a la parte de la recta comprendida entre dos puntos. Los puntos A y B limitan al segmento y se denominan extremos.
SEGMENTOS CONCATENADOS Y SEGMENTOS CONSECUTIVOS
Segmentos concatenados: dos segmentos con un extremo común y ningún otro punto común.
Segmentos consecutivos: segmentos concatenados que se encuentran sobre la misma recta.
POSICIONES RELATIVAS DE DOS RECTAS
Se trata de ver la posición que puede tener una recta respecto de otra.
Formamos grupos de cuatro personas. Cada grupo tendrá dos cuerdas. Cada cuerda la sujetarán dos alumnos por los extremos. Utilizaremos las cuerdas como representación de rectas, es decir, considerando su condición de infinitud. En cada grupo los alumnos analizarán de qué forma pueden colocarse las dos rectas sobre el suelo. Posteriormente se hará puesta en común y, si no se ha conseguido alguna de las posiciones relativas, se completará.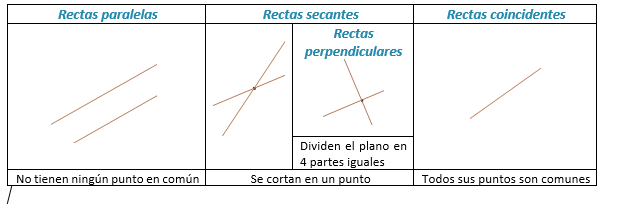 
TRAZADO DE RECTAS PARALELAS Y PERPENDICULARES A UNA RECTA
Dada una recta, colocando la escuadra y el cartabón como se muestra en la figura, puedes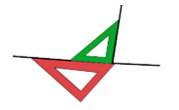 
dibujar una recta perpendicular a ella.
Dada una recta, colocando la escuadra y el cartabón como se muestra en la figura, y deslizando una sobre otra, puedes dibujar rectas paralelas a la recta de partida.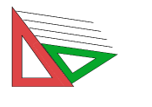 
DISTANCIA DE UN PUNTO A UNA RECTA
La distancia de un punto A a una recta r es la menor distancia que se recorre para ir desde el punto A a la recta r.
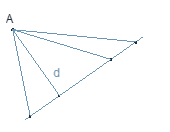Trabajamos en grupos de cuatro con dos cuerdas en cada grupo. Dos alumnos cogen una cuerda y, de esta forma, representan una recta. Otro alumno representa el punto A y, entre este alumno y el cuarto componente del grupo, cogen la otra cuerda. Este cuarto alumno va llevando la cuerda desde el punto A hasta diferentes puntos de la recta, tratando de encontrar cuándo se consigue la menor distancia.
La distancia de un punto a una recta es la longitud del segmento perpendicular desde el punto a la recta.
