LÍNEAS POLIGONALES
-
En los trayectos realizados hemos seguido lo que denominamos líneas poligonales
- Líneas poligonales
-
Conjunto de varios segmentos concatenados cada uno con el siguiente.
Pueden ser abiertas o cerradas como se indica en el gráfico:
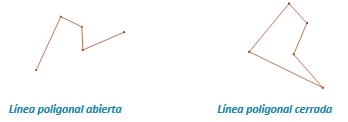
Los segmentos que componen cada línea poligonal se llaman lados y sus extremos se llaman vértices.·
-
- Diferencia entre las líneas poligonales abiertas y cerradas:
-
En la poligonal abierta para ir de un punto M a otro N el camino es único. En cambio, en la poligonal cerrada hay dos caminos distintos.
· La poligonal cerrada tiene un interior y un exterior separados por la línea poligonal, que es la frontera entre ambas.
· La poligonal abierta no tiene interior ni exterior. Si se quiere salir de un punto interior a otro exterior, sin salir del plano, es preciso atravesar la frontera (los lados).
POLÍGONOS
Un polígono es la región del plano que queda delimitada por una línea poligonal cerrada. La palabra polígono es una palabra de origen griego: poli- significa varios y -gono significa ángulo.
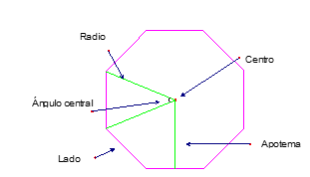
Elementos de un polígono
- Lados:
-
Segmentos que delimitan el polígono
- Vértices:
-
Extremos de los segmentos que forman los lados.
- Diagonal:
- Segmento que une dos vértices no consecutivos
- Ángulo interior
-
Ángulo formado por dos lados consecutivos del polígono
- Ángulo exterior
- Ángulo formado por un lado y la prolongación del lado consecutivo.
-
Clasificaciones
Los polígonos se pueden clasificar atendiendo a distintos criterios.
a) En función del número de lados o de ángulos interiores:
Triángulos (3 lados), cuadriláteros (4 lados), pentágonos (5 lados), hexágonos (6 lados), heptágonos (7 lados), octógonos (8 lados), eneágonos (9 lados), decágonos (10 lados), undecágonos o endecágonos (11 lados) y dodecágonos (12 lados). Para nombrar polígonos de más de 12 lados se dice: polígono de 13 lados, 14 lados, etc.
b) En función de la amplitud de sus ángulos interiores
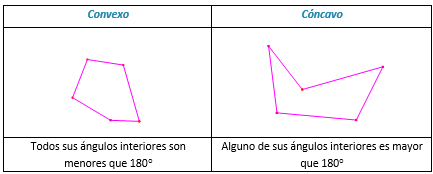
POLÍGONO REGULAR
Un polígono es regular si sus lados y sus ángulos son iguales. Si tiene algún lado o algún ángulo diferente, se dice que es un polígono irregular.

-
Elementos de un polígono regular
-
Centro: Punto que está a la misma distancia de todos los vértices.
Apotema: Segmento que une el centro con el punto medio de un lado.
Radio: Segmento que une el centro con un vértice.
Ángulo central: Ángulo determinado por dos radios consecutivos.
-
Observación de polígonos con un libro de espejos
-
Traza una línea recta y coloca el libro de espejos sobre ella como se indica en la siguiente figura. Abriendo y cerrando el libro de espejos, ¿qué figuras observas?
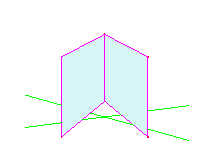
Traza dos líneas rectas secantes y coloca el libro de espejos como se indica en la imagen siguiente. ¿Qué observas?

EJE DE SIMETRÍA
Un eje de simetría de un polígono es una recta que divide al polígono en dos partes iguales de forma que una parte es reflejo de la otra
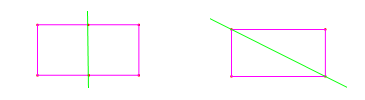
Determinación de un eje de simetría.
La recta trazada sobre ambas figuras divide al rectángulo en dos partes iguales. Sin embargo, la recta trazada en el rectángulo uniendo los puntos medios de sus lados opuestos es un eje de simetría, mientras que la diagonal del rectángulo no lo es. Podemos comprobarlo utilizando el doblado de papel.
NÚMERO POLIGONAL
Un número poligonal es un número natural que puede representarse geométricamente utilizando polígonos regulares. Los números poligonales se nombran en función del polígono regular utilizado: números triangulares, cuadrados, pentagonales, hexagonales, etc.