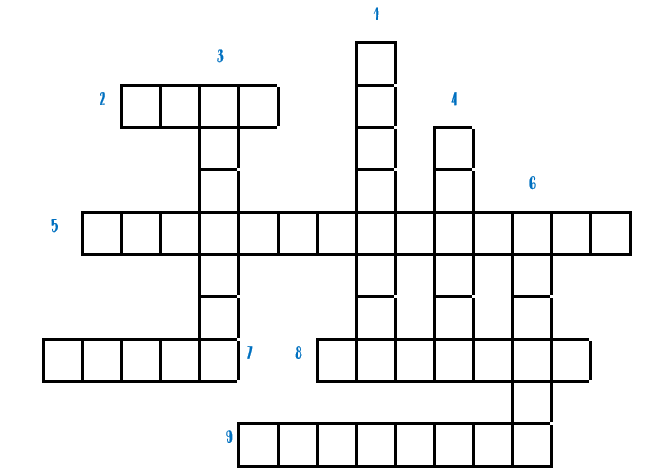
3.1.- Crucigrama. Completa con los elementos de la circunferencia.
HORIZONTALES
2. Es una porción de la circunferencia.
5. Línea curva cerrada y plana.
7. Distancia del centro a cualquier punto de la circunferencia.
8. Recta que corta a la circunferencia en dos puntos.
9. Es dos veces el radio.
VERTICALES
1. Recta que toca a la circunferencia en un solo punto.
3. Recinto delimitado por una línea curva cerrada y plana.
4. Segmento que une dos puntos de la circunferencia.
6. Punto que está a la misma distancia de todos los puntos de la circunferencia.
3.2.- Volvamos a la circunferencia que hicimos. Marca un radio y un diámetro.
-
Si el radio de la circunferencia fuese de 2 cm, ¿cuánto valdría su diámetro?
-
¿A qué distancia del centro están todos los puntos de la circunferencia del apartado anterior?
-
¿Cuántos radios pueden dibujarse en la circunferencia?
3.3.- La llanta de una bicicleta de montaña tiene 58 cm de diámetro. ¿Cuánto miden los radios de la rueda?
3.4.- Trazamos una cuerda en una tortilla de patata y la cortamos por ella.

a) ¿En cuántas porciones cómo máximo, no necesariamente iguales, quedaría dividida una tortilla si la cortas por dos cuerdas?
b) Rellena la siguiente tabla:

3.5.- Una piscina con forma circular de 4 metros de diámetro, tiene una isla circular con un radio de medio metro. ¿Qué figura representaría la piscina vista desde arriba?
¿Podía meter un niño una barca hinchable de forma circular de 15 dm de radio y flotar tranquilamente?
3.6.- Cortamos una tortilla de patatas en porciones con diferentes formas. Clasifica las porciones según el ángulo de corte realizado en cada porción.

3.7.- Dibuja una circunferencia de radio 3 cm. Marca un ángulo central y uno inscrito. ¿Cuánto mide cada uno?
3.8.- Dibuja una circunferencia y tres rectas: una secante, una tangente y una exterior.
-
Medimos el radio de la circunferencia
-
Medimos la distancia de cada recta al centro de la circunferencia.
-
¿Qué relación guarda esa distancia con el radio en cada caso?
3.9.- Dibuja una circunferencia de 2,5 cm de radio y dos rectas tangentes a ella y paralelas entre sí.
3.10.- Dibuja cada una de las posiciones relativas de dos circunferencias. En cada caso, medimos los radios de ambas circunferencias y anotamos si es mayor o menor siguiendo el esquema siguiente.
