1.1.- Utilizando regletas, pajitas o limpiapipas construye segmentos concatenados, consecutivos y otros que no lo sean.
1.2.- Señala, en el aula, dónde observas rectas paralelas, secantes o perpendiculares.
1.3.- Señala dónde está presente el paralelismo en la vida cotidiana.
1.4.- Consideramos una recta r y un punto A que no pertenece a dicha recta, es decir, A es un punto exterior a la recta. ¿Cuántas rectas puedes trazar que pasen por A y sean paralelas a la recta r?
1.5.- Dibuja dos rectas perpendiculares, r y s. ¿Se puede dibujar una recta que corte a r y no corte a s?
1.6.-¿Cómo calcularías la distancia entre dos rectas paralelas?
1.7.- Observa la imagen. Señala la posición relativa en la que se encuentran las siguientes calles:
a) Calle Alonso de Mercadillo y Calle Bellavista.
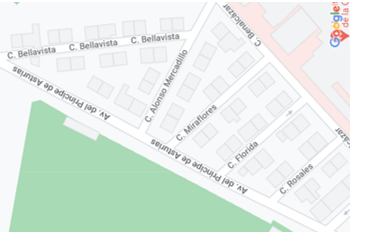
b) Calle Alonso de Mercadillo y Avda. Príncipe de Asturias.
c) Calle Miraflores y Calle Florida.
1.8.- Señala dos calles que se encuentren en las posiciones señaladas y que no coincidan con los pares de calles dados en los distintos apartados del ejercicio anterior
a) Paralelas.
b) Secantes.
c) Perpendiculares.
1.9.- Actividades sobre la definición de ángulo:
- Comprueba doblando un folio que: un ángulo es la región común a dos semiplanos definidos por dos rectas secantes.
- Un ángulo es la región del plano que barre una semirrecta al girar alrededor de su origen. La posición inicial y la final de la semirrecta determinan el ángulo.
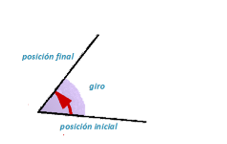
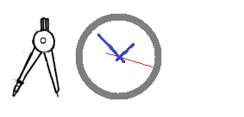
Son semirrectas que determinan ángulos, por ejemplo: La semirrecta que contiene la aguja minutero del reloj o el brazo de un compás. Encuentra algún ejemplo más.
1.10- Señala y cuenta los ángulos que aparecen en la palabra:

1.11- Demostración de que dos ángulos opuestos por el vértice son iguales:
Construye doblando un folio un par de ángulos opuestos por el vértice y dobla después el folio de forma que queden superpuestos. ¿Qué observas? ¿Coinciden? ¿Son ángulos iguales?
1.12- Dibuja un par de rectas que se corten y contesta a las preguntas:
- ¿Qué observas? ¿Cuántos ángulos quedan determinados? ¿Cuáles son iguales entre sí?
- ¿Se puede afirmar que: ¿Dos rectas que se cortan en un punto determinan dos pares de ángulos opuestos por el vértice, iguales dos a dos? Razona la respuesta
1.13-¿Cómo medirías un ángulo cóncavo con un transportador?
1.14- Repasa la teoría, y relaciona los ángulos por parejas o conjuntos atendiendo a alguna característica común o alguna relación entre ellos.
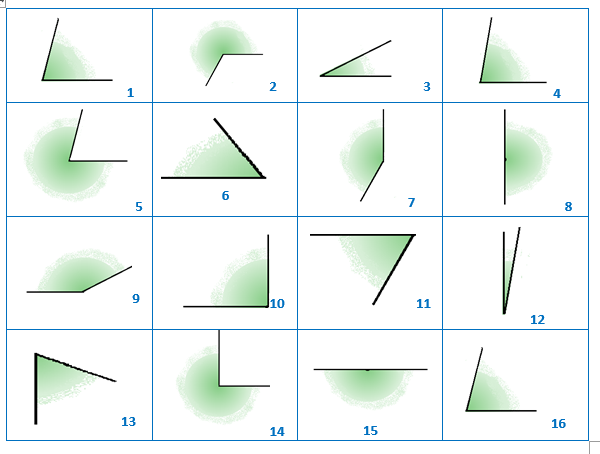
1.15.- Construye doblando papel, un ángulo de 90º, 45º, 135º, 180º, 225º y 270º.
Construye doblando papel y con el menor error posible, un ángulo de: 30º, 60º, 120º y 160º. Comprueba la medida de tus ángulos y anota el error que has cometido.
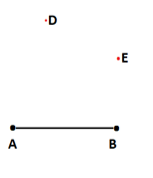
1.16.- En un partido de fútbol, un delantero se encuentra en el punto D y otro en un punto E. La portería está representada por el segmento AB. ¿Cuál de los dos delanteros tiene más ángulo de tiro? Comprueba tu respuesta usando un transportador de ángulos.
1.17.- Si un ángulo mide el doble que otro y ambos ángulos son complementarios. ¿Cuánto miden? Haz un dibujo que represente la situación.
1.18.- Si un ángulo mide la tercera parte que su suplementario. ¿Cuánto mide el ángulo ? Haz un dibujo que represente la situación.
1.19.- Los ángulos de una escuadra miden 45°, 45° y 90°, y los ángulos de un cartabón miden 30°, 60° y 90°.
Con esta información, observa las imágenes y calcula los ángulos indicados