TRIÁNGULOS
- Triángulo
-
Un triángulo es un polígono de tres lados. Para nombrar los vértices de un triángulo se usan letras mayúsculas y para los lados letras minúsculas, de forma que a un vértice y a un lado opuestos les corresponde la misma letra. Nombraremos los vértices, y por tanto los lados, siguiendo el sentido contrario al de las agujas del reloj. Un triángulo como el de la imagen se nombra: triángulo ABC
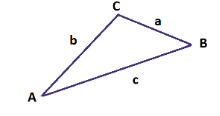
Un triángulo tiene tres vértices y tres ángulos. y además cualquier polígono con tres vértices o tres ángulos es un triángulo. Los triángulos son los polígonos más sencillos pero los más especiales. Por ejemplo, son los únicos que no tienen diagonales. Además, cualquier otro polígono se puede descomponer en triángulos. Conocer los triángulos es fundamental para el estudio de cualquier polígono.
- Relaciones entre los elementos de un triángulo:
-
En el Departamento de Matemáticas hemos construido un dibujador de triángulos como el de la figura. Utilízalo dibujar triángulos diferentes y para comprobar que:

En todo triángulo cada lado es menor que la suma de los otros dos y mayor que su diferencia
En todo triángulo el lado mayor se opone al ángulo mayor y el lado menor se opone al ángulo menor.
Recorta varios triángulos y comprueba doblando el papel como el de la figura que:
Los ángulos interiores de un triángulo suman 180°
Demostración usando geometría de plegado de papel.
- Construcción de triángulos
-
Veamos qué tengo que saber de un triángulo para poderlo construir. Si conocemos solo un elemento, un lado o un ángulo, es obvio que no tenemos información suficiente para dibujar el triángulo:

Si conocemos dos elementos:

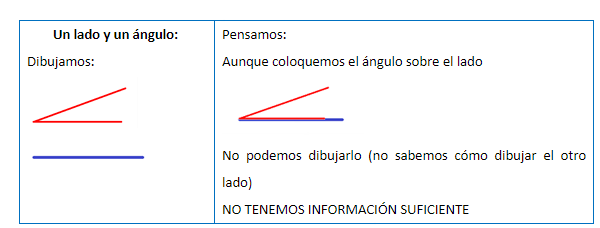
Si conocemos tres elementos:

- Determinación de un triángulo.
-
Dos triángulos son iguales si al superponerlos coinciden.

OBSERVA: Dos triángulos iguales tienen lados y ángulos respectivamente iguales.
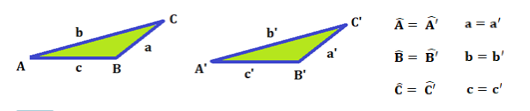
- Comparación de triángulos.
-
Para comparar dos triángulos no tenemos que comparar todos sus elementos
Dos triángulos son iguales si: Tienen los lados respectivamente iguales.
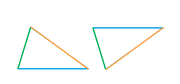
Tienen un lado y los ángulos contiguos a él respectivamente iguales
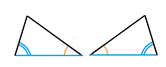
Tienen dos lados y el ángulo que forman respectivamente iguales
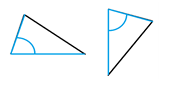
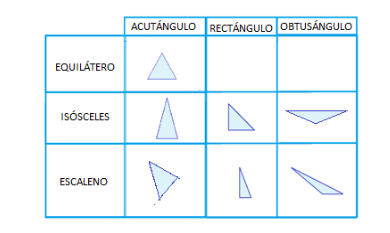
- Clasificación de los triángulos
-
Los triángulos se pueden clasificar atendiendo a sus lados o a sus ángulos.

El triángulo de la figura tiene los tres lados iguales, es equilátero.
El triángulo de la figura tiene al menos dos lados iguales, es isósceles.
El triángulo de la figura es equilátero e isósceles.
Todo triángulo equilátero es isósceles. Algunos triángulos isósceles son equiláteros.
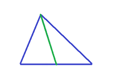
MEDIANAS Y BARICENTRO
- Mediana
-
Segmento que une un vértice con el punto medio del segmento que forma el lado opuesto. Un triángulo tiene tres medianas puesto que tiene tres lados.
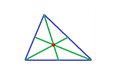
- Baricentro.
-
Las tres medianas de un triángulo se cortan en un punto llamado Baricentro.
- Trazado de las medianas y el baricentro
-
Con regla y compas:
Señalar el punto medio de un lado
Unir el punto medio del lado con el vértice opuesto.
Doblando papel:
Recortar un triángulo.
Doblar el triángulo para encontrar el punto medio del lado.
Hacer un doblez por el punto medio y el vértice opuesto.
Marcar el doblez. el segmento marcado es la mediana.
ALTURAS Y ORTOCENTRO
- Altura:
-
Segmento perpendicular a un lado que une ese lado o su prolongación con el vértice opuesto. Un triángulo tiene tres alturas, puesto que tiene tres lados
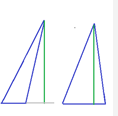
- Ortocentro.
-
Las tres alturas de un triángulo se cortan en un punto llamado ortocentro.
- Trazado de las alturas y el ortocentro
-
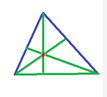
Con escuadra y cartabón:
Trazar una perpendicular a un lado que pase por el vértice opuesto, prolongar el lado si es necesario
Doblando papel:
Recortar un triángulo acutángulo.
Doblar el triángulo ayudándonos de la escuadra (o de otro folio que nos marque el ángulo recto) para encontrar la perpendicular al lado que pase el vértice opuesto.
Marcar el doblez. el segmento marcado es la altura
-
Repitiendo el procedimiento sobre los otros lados se dibujan las otras dos mediatrices. Para encontrar el circuncentro se marcan las tres mediatrices y se señala el punto donde se cortan.
MEDIATRICES, CIRCUNCENTRO Y CIRCUNFERENCIA CIRCUNSCRITA
- Mediatriz
-
Recuerda que la mediatriz de un segmento está formada por puntos que están a la misma distancia de los extremos del segmento.
Mediatriz: mediatriz del segmento que forma el lado. Un triángulo tiene tres mediatrices puesto que tiene 3 lados que son segmentos.
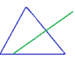
- Circuncentro
-
Las tres mediatrices de un triángulo se cortan en un punto llamado circuncentro.
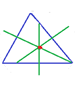
- Trazado de las mediatrices y el circuncentro.
-
Con regla y compás:
Trazar la mediatriz de un lado.
Doblando papel:
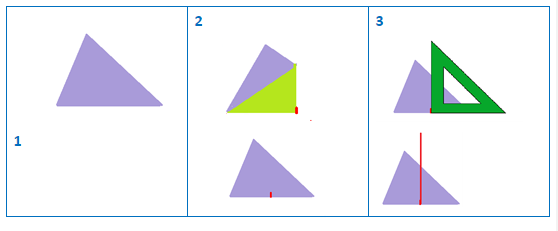
Recortar un triángulo.
Doblar el triángulo para encontrar el punto medio del lado y marcarlo.
Doblar el triángulo ayudándonos de la escuadra (o de otro folio que nos marque el ángulo recto) para encontrar la perpendicular al lado que pase el punto medio del lado.
Marcar el doblez. el segmento marcado es la mediatriz
Repitiendo el procedimiento sobre los otros lados se dibujan las otras dos mediatrices. Para encontrar el circuncentro se marcan las tres mediatrices y se señala el punto donde se cortan.
- Circunferencia circunscrita
-
Cuando trazamos las mediatrices de un triángulo el circuncentro está a la misma distancia de los tres vértices porque está en las tres mediatrices. Si hacemos una circunferencia pinchando el compás en el circuncentro y lo abrimos para tomar la distancia a uno de los vértices, la circunferencia que obtenemos pasa por todos los vértices. Se llama circunferencia circunscrita porque rodea al triangulo.
BISECTRICES,INCENTRO Y CIRCUNFERENCIA INSCRITA
- Bisectriz
Recuerda que la bisectriz de un ángulo está formada por puntos que están a la misma distancia de los lados del ángulo.
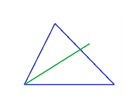
- Incentro
-
Las tres bisectrices de un triángulo se cortan en un punto llamado incentro. Cuando trazamos la bisectriz de un triángulo el incentro está a la misma distancia de los tres lados porque está en las tres bisectrices.
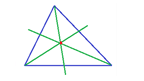
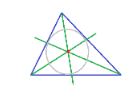
- Circunferencia inscrita
-
Si hacemos una circunferencia pinchando el compás en el incentro y lo abrimos para tomar la distancia a uno de los lados, la circunferencia que obtenemos es tangente a todos los lados . Se llama circunferencia inscrita porque está dentro del triángulo.
- Trazado de las bisectrices y el incentro
-
Con escuadra y cartabón:
Trazar la bisectriz del ángulo interior del triángulo.
Doblando papel:
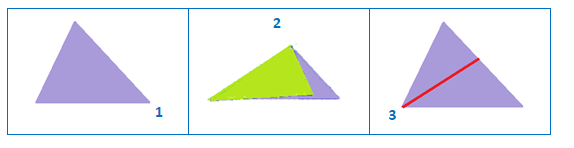
Recortar un triángulo.
Hacer un doblez en el triángulo que pase por el vértice y divida al ángulo en dos parte iguales.
Marcar el doblez. el segmento marcado es la bisectriz.

Repitiendo el procedimiento sobre los otros lados se dibujan las otras dos bisectrices. Para encontrar el incentro se marcan las tres bisectrices y se señala el punto donde se cortan.
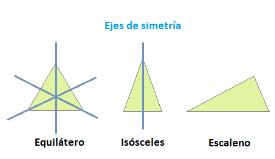
ESTUDIO DE LOS EJES DE SIMETRÍA DE UN TRIÁNGULO
Estudiamos los ejes de simetría con la geometría del plegado.
El triángulo equilátero lo podemos doblar de tres formas para que se superponga exactamente una mitad sobre la otra. Tiene tres ejes de simetría que coinciden también con sus medianas alturas mediatrices y bisectrices.
El triángulo isósceles no equilátero solo lo podemos doblar de una forma para que se superponga exactamente una mitad sobre la otra. Tiene un eje de simetría que coincide con la altura, mediana, la mediatriz y la bisectriz que cortan el lado desigual.
El triángulo escaleno no tiene ejes de simetría.